本文是一篇工程管理论文,本文以岳城煤矿Ⅲ1301 工作面地表移动监测站实测数据成果为基础和依据,实测数据成果是监测点的三维数据变形情况,通过基础分析和残余变形理论结合,可以得出以下结论:1.卡尔曼滤波理论在开采移动变形预计上是完全可行的,因为卡尔曼滤波被提出的主要目的就是为了解决动态数据处理问题。针对扩展卡尔曼滤波和标准卡尔曼滤波的通病-滤波发散问题进行自适应处理,构建极大后验自适应扩展卡尔曼滤波的数学模型,与其他滤波优劣性分析。监测点的数值变形情况非常复杂属于非线性预计分析,而极大后验过程对扩展卡尔曼滤波的初值问题和模型复杂问题进行简化,避免因为计算复杂出错和减小扩展卡尔曼滤波引入线性误差带来的结果精准度下降。
第1章 绪论
1.1 选题背景及研究意义
我国是煤炭资源需求大国,煤炭产量居世界首位。煤炭产业在我国经济中占有不可或缺的地位,煤炭资源的开采给社会带来了重大的经济效益[1]。各种产业结构随着我国社会快速进步和科技的飞速发展不断进行着改变,对基础能源的需求也来越大,所以对煤炭需求依然巨大。虽然新能源(例如核能和太阳能等)现在发展迅猛,未来一段时间内我国基础能源还是煤炭的格局近些年难以发生巨大改变。
煤炭的大规模开采势必会对开采沉陷区带来不可避免的危害。煤炭开采过程中引起的地表沉陷是目前开采沉陷区的主要灾害之一,不仅会破坏森林植被,损毁农田,形成泥石流灾害,还会加剧水土流失和荒漠化程度,引起地下水循环系统的改变。随着煤炭开采范围的加大,开采后地表沉陷范围将随之增加,对周围地质环境的影响亦随之增大。若开采影响范围内有建筑工程设施,还会对其造成一定程度上的损坏,甚至可能造成巨大的财产经济损失甚至人员伤亡。根据相关资料显示,我国由于采矿造成的地面坍塌约 70 万公顷,平均每年由于采矿造成的新增地面坍塌 0.2 公顷[2]。
目前阶段煤炭资源的获取在我国还是必不可少的一部分,随着我国经济建设的转型和对建设环境保护型社会的要求以及人们对于环境保护意识的提高,我国在煤炭开采问题上提出了许多要求和限制。为了既要绿水青山也要金山银山的科学规划,依据煤炭安全生产“十三五”规划和煤矿环境保护管理制度,需要提升煤矿的信息化程度,提前预测分析开采后的潜在危害和规划治理方案,减少对社会和环境造成的灾害。基于以上研究背景,针对在开采过程中的监测站监测点可能丢失和监测数据可能失准的问题,提出极大后验自适应扩展卡尔曼滤波算法。在开采沉陷监测过程中,卡尔曼滤波利用不断更新的监测数据,不断提高自身预计精度,进行动态预报,预测下一周期内监测点变化情况,从而提升预警机制。在监测结束时,开采沉陷过程进入衰退期,利用滤波及时、快速的对开采沉陷区地表残余变形情况进行分析,提前分析开采沉陷地表移动变形范围,从而为该地区提供一种周全的治理方案。
..........................
1.2 国内外研究现状
1.2.1 矿山开采沉陷研究现状
开采沉陷是指有用矿物被采出后,开采区域周围岩体的原始应力平衡遭到破坏,应力重新分布,达到新的平衡。在此过程中,使地表和岩层产生连续的移动、变形和非连续破坏,矿山开采引起的岩层与地表移动的过程十分复杂,它是许多地质采矿因素综合影响的结果。在二十世纪之前,哥特、依琴斯凯、耳西哈、高斯分别提出了法线理论、二等分线理论[3]、自然斜面理论[4]、高斯理论[5],这是最早开始对开采沉陷理论进行初步研究。进入二十世纪后,随着科学技术的飞速发展,人们对开采沉陷认知更加深入。首先由德国学者 Niemezyk 在 1949 年通过大量的实测数据进行煤炭开采引起地表移动变形规律分析,归纳总结出下沉、水平移动、曲率等曲线的绘制方式[6-7]。波兰学者 Knothe 和 Budryk 在模拟地表最终下沉时尝试加入正态分布作为基础影响函数。 在 1954 年,J.Litwiniszyn 提出概率积分法的雏形-使用随机介质理论引入开采沉陷过程中[8-11]。
我国在开采沉陷研究上起步较晚,在上世纪 60 年代初才开始相关系统性研究。刘宝琛和刘天泉等[12]学者开始把国外相对成熟的随机介质理论引入国内,才开始了系统性研究。1965 年概率积分法被首次提出,中国学者刘宝琛、廖国华[13-14]做出了巨大贡献,并为我国开采沉陷理论研究提供理论基础。随着我国矿业开采进入大爆发阶段,实测监测数据越来越多,我国学者着重研究覆岩层、工程地质条件等物理力学性质与预计参数的关系,对概率积分法的应用工作进行了系统性的总结、归纳分析[15-16]。
.......................
第2章 改进卡尔曼滤波算法和残余变形理论简介
2.1 卡尔曼滤波简介
在卡尔曼滤波被提出之前,最先提出最初的线性滤波理论是维纳滤波理论。该滤波的最大缺点是只能应用在已完成的数据工作研究中,不能进一步预测和实时处理数据。之后在 1960 年,由 Kalman 把状态空间模型引入滤波理论,利用线性无偏差最小方差估计原理在概率论和数理统计理论下对有限的时间序列数据进行最优线性估计[65],通过剔除观测数据中系统噪声和干扰的影响,拿这种最优估计作为滤波过程,并推导出滤波计算公式,后人为了纪念他做出的贡献,称为卡尔曼滤波(也称作 Kalman Filtering 简称 KF)[66],在通讯、导航、制导与控制等多领域得到了较好的应用与发展。

.......................
2.2 卡尔曼滤波(KF)模型
2.2.1 卡尔曼滤波基础模型
卡尔曼滤波(Kalman Filtering)可以运用在任何含有不确定信息动态系统中,不仅因为滤波主要是在时间域上进行表述分析,且可以根据系统的接下来要进行走向做出有根据的预计。因为滤波是在线性系统的状态空间基础上,根据观测数据对随机量进行定量推断。滤波主体分为系统状态预测和系统状态更新两个过程。也就是根据之前的数据分析提出对系统作用的参数,该参数分为系统噪声和观测噪声。通过最优估计理论和滤波自身不断递推,滤波值不断接近真实值,使得滤波成为一种最优化自回归数据的处理算法[67]。
Kalman 滤波是一种动态数据处理递推算法,算法不需要处理系统中以前储存的数据[68],只需要处理系统每一时刻的最新量测值,利用系统状态噪声和观测噪声的统计学特性,用概率论与数理统计理论得到系统的线性最优估计[69]。Kalman滤波利用目标的动态信息与观测结果相结合,抑制噪声的影响,获得一个估计值,这个估计值针对应用中的实际分析,可以是对过去、现在和未来的估计。而且滤波基本方程是时间域内的递推过程,非常适合实时处理分析数据。开采沉陷监测数据会实时更新,卡尔曼滤波符合这一特性。所以其应用范围是十分广泛的[70],如雷达测距、图像采集、声呐感应等,测量得出数据和传感器接收数据等,这些数据都是带有噪声干扰的。这种影响有的是很微小,有的则会是信号变形、失真,有的严重导致数据不能使用。但是卡尔曼滤波也不是万能的,只能最大限度的降低噪音的干扰获得更加精确的值。
...........................
第 3 章 基于Ⅲ1301 工作面的改进滤波预测分析 .....................29
3.1 Ⅲ1301 工作面简介.........................29
3.2 确定滤波初值.................................31
第 4 章 基于极大后验自适应扩展卡尔曼滤波的残余变形分析...............63
4.1 走向残余变形下沉值分析..............................63
4.2 走向残余变形水平移动值分析...................................68
第 4 章 基于极大后验自适应扩展卡尔曼滤波的残余变形分析
4.1 走向残余变形下沉值分析
在开采完成后的残余变形期的预计分析过程中,先利用理论预计方程分析该地区的残余变形过程,再结合 17 期实测数据构建极大后验自适应扩展卡尔曼滤波,通过理论结果分析极大后验自适应扩展卡尔曼滤波模型的正确性。
在进行卡尔曼滤波模拟计算开采沉陷过程中残余变形之前,首先应用残余变形预计理论对山西岳城矿区山区Ⅲ1301 工作面进行分析。
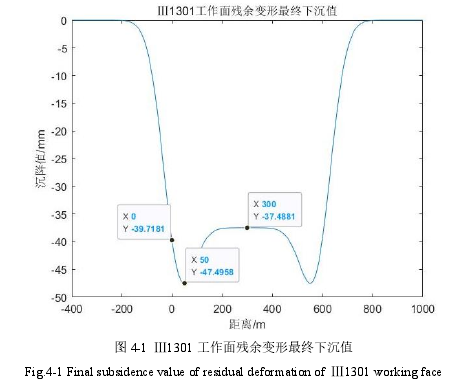
工作面基本信息为:煤层倾角α = 6°,煤层厚度 m=2.65。根据实际观测资料计算,下沉系数 q 为 0.78,影响传播角θ = 88°,主要影响正切值tanθ = 2.6,拐点偏距 0= 24m,水平移动系数 b=0.15,主要影响半径 r=148m,开采完成后等价采厚 m1=0.583m。利用公式(2-6)计算出该地区最终残余变形值,绘制曲线如图 4-1 所示。
...........................
结论与展望
结论
本文以岳城煤矿Ⅲ1301 工作面地表移动监测站实测数据成果为基础和依据,实测数据成果是监测点的三维数据变形情况,通过基础分析和残余变形理论结合,可以得出以下结论:
1.卡尔曼滤波理论在开采移动变形预计上是完全可行的,因为卡尔曼滤波被提出的主要目的就是为了解决动态数据处理问题。针对扩展卡尔曼滤波和标准卡尔曼滤波的通病-滤波发散问题进行自适应处理,构建极大后验自适应扩展卡尔曼滤波的数学模型,与其他滤波优劣性分析。监测点的数值变形情况非常复杂属于非线性预计分析,而极大后验过程对扩展卡尔曼滤波的初值问题和模型复杂问题进行简化,避免因为计算复杂出错和减小扩展卡尔曼滤波引入线性误差带来的结果精准度下降。
2.采用卡尔曼滤波对岳城煤矿Ⅲ1301 工作面的监测数据进行预计和实际监测数据对比分析,采用前 8 组数据进行训练自适应性,中间 5


